OpenGL坐标系统与渲染管线

前言

　　图形学中最基础的东西就是坐标系统，三维的东西如何在二维中显示，这中间经历了数次坐标变换，同时坐标变换也贯穿了整个计算机图形渲染管线。

坐标篇

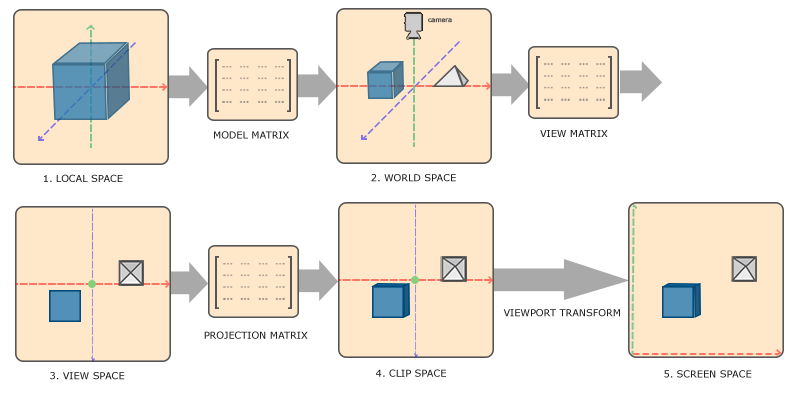
　　在计算机图形世界中，为更灵活的控制三维物体显示在二维中，将变换的过程大致分为 5 个空间：1、局部空间（Local Space，或者称为物体空间（Object Space））；2、世界空间（World Space）；3、观察空间（View Space，或者称为视觉空间（Eye Space））；4、裁剪空间（Clip Space）；5、屏幕空间（Screen Space）。局部空间中是物体相对于坐标原点的坐标，也是物体的固有坐标，在依次经历过缩放旋转平移，也即模型矩阵（Model Matrix）变换后，物体局部坐标变换为世界坐标，世界坐标中即定义了物体所在的位置，以及产生的旋转和缩放。在世界空间中加入相机，以相机的视角看世界中的物体，即通过观察矩阵（View Matrix，也称视图矩阵）变换后，将世界坐标转换为观察坐标，由于一张屏幕能显示的东西是有限的，而三维世界中的物体是无限，所以需要通过投影矩阵（Projection Matrix）对三维空间进行裁剪，以决定哪些物体能显示在屏幕上，为方便的计算机判断，处于裁剪空间内的坐标会被转换为 [-1, 1]，为顺利在屏幕上显示，又需要通过视窗变换（Viewport Transform）将 [-1, 1] 映射为 viewport 中的图元坐标，再通过渲染管线的其他流程输出为屏幕上的像素点。

变换篇

　　矩阵相乘一般有左乘和右乘之分，左乘和右乘的区别在于坐标是按列还是按行排列（OpenGL 中是按列，所以是左乘，DX 中按行，所以是右乘，同一种变换，传入 DX 中的矩阵与传入 OpenGL 中的矩阵互为转置），坐标与矩阵相乘越靠近坐标的矩阵表示该坐标越先做相应矩阵变换。

　　模型矩阵，视图矩阵，投影矩阵，在简单的顶点着色器编程中，这三个矩阵一般会合并成一个 MVP 矩阵传入 GPU 中。

模型矩阵

　　模型矩阵一般定义了物体的缩放旋转平移状态，缩放矩阵的构造很简单，若物体在 \((x,y,z)\) 方向上缩放尺度分别为 \((S_x, S_y, S_z)\)，则缩放矩阵为： \[ M_{scaling} = \begin{bmatrix} S_x & 0 & 0 & 0 \\ 0 & S_y & 0 & 0 \\ 0 & 0 & S_z & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix} \] 　　旋转矩阵就非常麻烦了，这里暂且不讨论其如何计算，只给出矩阵，物体绕任意轴 \((R_X, R_y, R_z)\) 旋转 θ 角的矩阵为： \[ M_{rotation} = \begin{bmatrix} cos\theta+R_x^2(1-cos\theta) & R_xR_y(1-cos\theta)-R_zsin\theta & R_xR_z(1-cos\theta)+R_ysin\theta & 0 \\ R_yR_x(1-cos\theta)+R_zsin\theta & cos\theta+R_y^2(1-cos\theta) & R_yR_z(1-cos\theta)-R_xsin\theta & 0 \\ R_zR_x(1-cos\theta)-R_ysin\theta & R_zR_y(1-cos\theta)+R_xsin\theta & cos\theta+R_z^2(1-cos\theta) & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix} \] 　　当然，由于万向节锁的存在，一般不会直接使用欧拉角和旋转轴计算旋转矩阵，而是会通过四元数得到旋转矩阵，这样既高效又能避免万向节锁，详情可看「LearnOpenGL」译者的教程。

　　至于平移矩阵也非常简单，若物体在 \((x,y,z)\) 方向上平移量分别为 \((T_x, T_y, T_z)\)，则平移矩阵为： \[ M_{translation} = \begin{bmatrix} 1 & 0 & 0 & T_x \\ 0 & 1 & 0 & T_y \\ 0 & 0 & 1 & T_z \\ 0 & 0 & 0 & 1 \end{bmatrix} \] 　　前面的缩放和旋转矩阵其实只需要用到 3×3 的矩阵，而之所以用 4×4 的表示也是因为平移矩阵，普通的 3 维坐标必须增加一维 \(w\) 构成齐次坐标才能进行平移操作，\(w\) 一般都是 1.0，而从齐次坐标\((x,y,z,w)\) 变为普通的 3 维坐标需要每个分量除以 \(w\)，即 \((x/w, y/w, z/w)\) 。

则模型矩阵 \(M_{model} = M_{translation} \cdot M_{rotation} \cdot M_{scaling}\)。

视图矩阵

　　视图矩阵描述的是三维场景中模拟相机的状态，根据模拟相机的状态确定一套以相机为原点的相机坐标系，从而使用视图矩阵进行坐标变换，至于为啥是模拟相机，是因为 OpenGL 本身并没有相机的概念，通过模拟相机来实现在三维场景中的漫游。

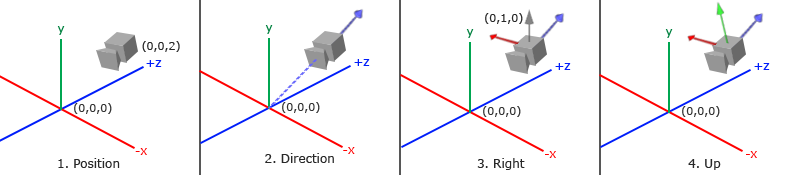
　　模拟相机有三个关键点，分别为相机位置（cameraPos），相机朝向点（cameraTarget），相机上向量（top），根据相机位置和相机朝向点可确定相机坐标系的 z 轴正向向量 \(cameraDirection = (cameraPos - cameraTarget).normalize\)，叉乘相机上向量和相机 z 轴正向向量可得到相机坐标系 x 轴正向向量 \(cameraRight = top.cross(cameraDirection).normalize\)，最后将相机 z 轴正向向量与 x 轴正向向量叉乘得到 y 轴正向向量 \(cameraUp = cameraDirection.cross(cameraRight)\)，如此即可建立完整的相机坐标系，从而得到变换矩阵，即视图矩阵： \[ M_{view} = \begin{bmatrix} R_x & R_y & R_z & 0 \\ U_x & U_y & U_z & 0 \\ D_x & D_y & D_z & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} 1 & 0 & 0 & -P_x \\ 0 & 1 & 0 & -P_y \\ 0 & 0 & 1 & -P_z \\ 0 & 0 & 0 & 1 \end{bmatrix} \] 其中 \(R\) 是相机 x 轴正向向量，\(U\) 是相机 y 轴正向向量，\(D\) 是相机 z 轴正向向量， \(P\) 是相机位置向量。

投影矩阵

　　投影矩阵描述的是摄像机前的可视区域（Frustum），根据可视区域的形状可分为正射投影（Orthographic Projection）和透视投影（Perspective Projection）。

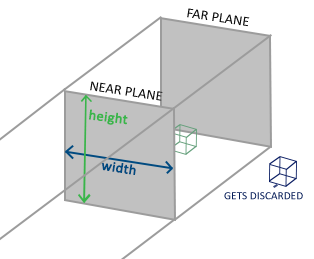
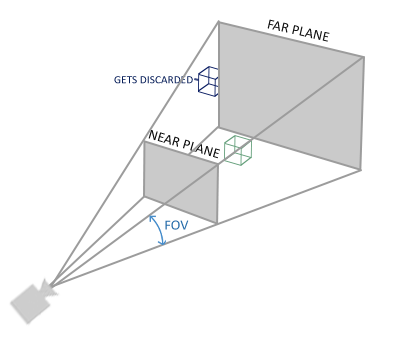
orthographic projection frustum perspective_frustum

　　对于这两种投影，都有远（far）近（near）参数，不同的是，正射投影是个立方体，所以有左（left）右（right）上（top）下（bottom）四个参数，而透视投影是个类梯形台，所以还有垂直方向视野（Field of View，fov），以及一个宽高比（aspect）两个参数。远近两个参数决定摄像机能看到多近和多远的物体，太近和太远都会看不见，一般可设 near = 0.1，far = 1000；若渲染视窗（viewport）宽为 W，高为 H，则一般 \(left=-W/2, right=W/2, top=H/2, bottom=-H/2\) ；透视投影的 fov 是角度，一般设为 45.0，而 \(aspect = W/H\) 。这两种投影的矩阵分别为： \[ M_{orth} = \begin{bmatrix} \frac{2}{right-left} & 0 & 0 & -\frac{right+left}{right-left} \\ 0 & \frac{2}{top-bottom} & 0 & -\frac{top+bottom}{top-bottom} \\ 0 & 0 & \frac{-2}{far-near} & -\frac{far+near}{far-near} \\ 0 & 0 & 0 & 1 \end{bmatrix} \\ M_{pers} = \begin{bmatrix} \frac{2near}{right-left} & 0 & \frac{right+left}{right-left} & 0 \\ 0 & \frac{2near}{top-bottom} & \frac{top+bottom}{top-bottom} & 0 \\ 0 & 0 & \frac{-(far+near)}{far-near} & \frac{-2far*near}{far-near} \\ 0 & 0 & -1 & 0 \end{bmatrix} \]

　　在 three.js 中，对于透视投影矩阵中 left, right, top, bottom 计算方式为：

let top = near * Math.tan( _Math.DEG2RAD * 0.5 * this.fov ) / this.zoom;
let height = 2 * top;
let width = this.aspect * height;
let left = - 0.5 * width;
let right = left + width;
let bottom = top - height;

　　对于透视投影，由于计算出的齐次坐标 w 分量显然不为 1.0，所以必须进行透视除法（x,y,z 各分量分别除以 w），得到真正的 3 维坐标。

　　正射投影一般用来模拟 2D 空间，透视投影用来模拟 3D 空间，当透视投影 near 和 far 设置的相差太大时，很容易引发 z-fighting 现象，原因是离近平面越远时，计算出的深度精度越低，three.js 中为解决这一问题，引入了一个 logarithmicDepthBuffer 参数来决定是否开启使用对数函数优化深度计算，具体可看源码中的 logdepthbuf_vertex.glsl.js 和 logdepthbuf_fragment.glsl.js 文件，开启该参数会造成渲染性能下降。

小结

　　\(M_{mvp} = M_{projection}M_{view}M_{model}\)，一个局部坐标 \(V_{local}\) 在经过 MVP 矩阵变换之后可得到裁剪坐标 \(V_{clip} = M_{mvp}V_{local}\) ，在 OpenGL 中，\(V_{clip}\) 会被赋值到顶点着色器中的 gl_Position，并且 OpenGL 会自动进行透视除法和裁剪。

　　3 维中的相机一般可分为两种，第一人称相机（常规 FPS 游戏）和第三人称相机（常规 ARPG 游戏），第一人称相机的特点是灵活，相机往往可以任意改变位置和朝向，所以会对某些人造成一种 “晕 3D” 的现象，而第三人称相机虽然可以改变相机朝向点和位置，但当朝向点和到朝向点的距离一旦固定，则相机只能沿着以朝向点为球心，以到朝向点的距离为半径的球面上运动，这两种相机一般看具体业务需求进行选择。

　　缩放操作是很常规的一种操作，镜头拉近代表放大，拉远代表缩小。在使用透视投影的 3 维场景中，只需要改变相机到朝向点的距离即可简单实现缩放操作，而在使用正射投影的场景中，改变距离并不能实现缩放，而是需要改变左右上下四个参数，所以在相机中往往会在引入一个 zoom 的参数，用左右上下四个参数分别除以 zoom 得到真正的左右上下，从而改变 zoom，就可以改变相机参数，进而实现正射投影的缩放。

管线篇

　　渲染管线，图形学中最重要的概念之一，既然称之为管线，自然有像流水线一样的步骤，各个步骤具体做的事情如下：

顶点着色器：负责将顶点数据进行坐标变换，该着色器中一般存在 MVP 矩阵，负责将三维坐标变换为二维坐标，该阶段也可以优化每个点的深度值，以便管线后续进行深度测试，也可以利用光照简单优化每个顶点的颜色；
图元装配：将输入的顶点数据进行组装，形成图元，常见的图元包括：点(GL_POINTS)、线(GL_LINES)、线条(GL_LINE_STRIP)、三角面(GL_TRIANGLES)，在该过程中，一般 GPU 会做一些裁剪和背面剔除等操作，以减少图元的数量，同时完成透视除法以进行屏幕映射；
光栅化：负责计算每个图元到屏幕像素点的映射。光栅化会计算每个图元所覆盖的片元，同时利用顶点属性插值计算每个片元的属性，片元可认为是候选像素，经过后续管线阶段即可变为真正的像素。
片元着色器：将光栅化得到的片元进行颜色计算。图形学中几乎所有的高级特效都会在这一步完成，光照计算，阴影处理，纹理，材质，统统在这一步进行处理；
归属测试：即测试片元所在位置是否位于当前上下文视窗内，若一个显示帧缓冲区视窗被另一个视窗所遮蔽，则剔除该部分片元。
模板测试：即测试片元是否满足一定条件（可大于或小于某个值等），若测试不满足，则剔除该该片元， OpenGL 可自行选择开启或关闭模板测试。
深度测试：用来测试片元的远近，远的片元被遮挡。在深度测试，若两片元深度值接近，则可能会引起 Z-fighting 现象，即像素闪烁，这是因为此时 GPU 无法确定该剔除哪个片元，导致这一帧可能绘制这个片元，下一帧绘制另一个片元。若开启 Alpha 测试，即启用透明度，则会在下一阶段进行 Alpha 混合，从而达到透明效果。
混合：将新生成的片元颜色和帧缓冲区中对应位置的颜色进行混合，得到像素颜色。
抖动：一种以牺牲分辨率为代价来增加颜色表示范围技术，从视觉效果上来看就是颜色过度更平滑。

　　以上这些阶段中，能完全被编程控制的也就顶点着色器和片元着色器两个阶段，其余阶段要么完全无法控制，要么只能通过已有的参数进行设置，当然也可以通过顶点着色器和片元着色器影响余下阶段，顶点着色器和片元着色器也统称 Shader 编程。

　　有时候为了做更好看的特效，需要进行多次渲染，将上一次渲染的结果作为下一次渲染的输入，此时可以将颜色缓冲区作为一张纹理，并构造新的帧缓冲区，将该纹理作为输入，重新放进渲染管线中，这种操作方式也叫后期处理（Post Processing），虽然好看，但对 GPU 的负载很大，需要合理使用。

　　对于渲染管线，Shaun 的理解也就到此为止了，非常粗浅，Shader 也只是刚入门的水平，Shaun 在图形学方面做的更多是降低 Draw-Call 和 CPU 层面的 Tessellation，以及 Geometry 上的事，对纹理材质颜色光照阴影等方面涉及的较少。

后记

　　虽然目前 OpenGL 已停止更新，但学习图形学编程，OpenGL 总是绕不过去（至少暂时以及未来很长一段时间都会是这样），而且图形学基础知识本质都是相同的，不管是 DirectX 还是 Vulkan，变的只是写法形式而已，数学知识总是在那里，两种 shader 也同样需要，所以了解这些东西还是有必要的。

附录

二维图像的图像透视投影变换

　　图像的透视投影变换常用于图像的矫正，OpenCV 中就有现成的 api（getPerspectiveTransform 和 warpPerspective），用于将不规整的四边形区域变换为规整的矩形区域。其基本的数学原理为，先构造一个投影变换等式： \[ \begin{bmatrix} XW \\ YW \\ W \end{bmatrix} = \begin{bmatrix} a & b & c \\ d & e & f \\ g & h & 1 \end{bmatrix} \begin{bmatrix} x \\ y \\ 1 \end{bmatrix} \] 设四边形中四个点分别为 \((X_1, Y_1),(X_2, Y_2),(X_3, Y_3),(X_4, Y_4)\) ，对应矩形中四个点为 \((x_1, y_1),(x_2, y_2),(x_3, y_3),(x_4, y_4)\)。则可构造齐次线性方程组： \[ \begin{bmatrix} x_1 & y_1 & 1 & 0 & 0 & 0 & -X_1x_1 & -X_1y_1 \\ 0 & 0 & 0 & x_1 & y_1 & 1 & -Y_1x_1 & -Y_1y_1 \\ x_2 & y_2 & 1 & 0 & 0 & 0 & -X_2x_2 & -X_2y_2 \\ 0 & 0 & 0 & x_2 & y_2 & 1 & -Y_2x_2 & -Y_2y_2 \\ \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots \\ x_n & y_n & 1 & 0 & 0 & 0 & -X_nx_n & -X_ny_n \\ 0 & 0 & 0 & x_n & y_n & 1 & -Y_nx_n & -Y_ny_n \end{bmatrix} \begin{bmatrix} a \\ b \\ c \\ d \\ e \\ f \\ g \\ h \end{bmatrix} = \begin{bmatrix} X_1 \\ Y_1 \\ X_2 \\ Y_2 \\ \vdots \\ X_n \\ Y_n \end{bmatrix} \] 解这个方程组得到 abcdefg ，使用上面的投影变换等式可计算 \(X = XW / W, Y = YW / W\) ，从而使用插值得到规整矩形图形的各个像素值。