矩阵的应用之图像仿射变换

前言

　　好像很久没写新的东西了，主要是最近期末有一大堆事情要做，忙着写各种结课论文和复习数学，又加上最近忙着把《奥日与黑暗森林：终极版》剧情通关，这游戏不管是画面还是音乐都特别棒，但是对键盘用户太不友好了，不能改键位，需要一只手控制键盘，一只手控制鼠标，如果只是普通的键位就算了，它还要万恶的 shift 键配合，手残党完全吃不消 (´･ω･`)。最终死亡 658 次好歹剧情通关了，最后悔的是没把三段跳点出来 /つ∇T)。这些事情一搞完，Shaun 这不就又开始写了嘛（说什么也摆脱不了你拖延症晚期的事实 (￣ε(#￣)☆╰╮(￣▽￣///) ）。选修的《数字图像处理》是也早结课了，虽然教的东西大都事前已经了解了，但是好像还没写过图像处理相关的 blog，所以谨以此篇最基础的 blog 来表示一下。

预备篇

　　首先需要了解的是图像中坐标系和数学课本中常用的坐标系略有不同，图像中坐标系是以左上角为原点，水平向右为 X 轴，垂直向下为 Y 轴；而数学课本中常见的坐标系是以图像中心为原点，水平向右为 X 轴，垂直向上为 Y 轴。所以由图像中坐标 $(x,y)$ 转数学课本中常见的坐标 $(x',y')$ 的公式为 $x' = x - C/2; y' = -y + R/2; $ 其中 $C$ 表示原图像总列数，即原图像宽度，$R$ 表示原图像总行数，即原图像高度。

　　※注：值得注意的是因为 MATLAB 和 OpenCV 的像素索引坐标形式为 (行坐标，列坐标) ，所以若以本文这样定的图像坐标，则图像中坐标 $(x,y)$ 对应的像素值为 $f(y,x)$。

变换篇

据 OpenCV 文档所说：

一个任意的仿射变换都能表示为 乘以一个矩阵 (线性变换) 接着再 加上一个向量 (平移).
综上所述, 我们能够用仿射变换来表示:
旋转 (线性变换)
平移 (向量加)
缩放操作 (线性变换)
你现在可以知道, 事实上, 仿射变换代表的是两幅图之间的关系 .
我们通常使用 $2$ 矩阵来表示仿射变换.
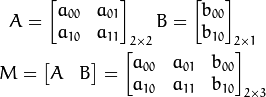
$A = \begin{bmatrix} a_{00} & a_{01} \\ a_{10} & a_{11} \end{bmatrix}_{2 \times 2} B = \begin{bmatrix} b_{00} \\ b_{10} \end{bmatrix}_{2 \times 1} M = \begin{bmatrix} A & B \end{bmatrix} =\begin{bmatrix} a_{00} & a_{01} & b_{00} \\ a_{10} & a_{11} & b_{10}\end{bmatrix}_{2 \times 3}$ 　　
考虑到我们要使用矩阵 $A$ 和 $B$ 对二维向量 $X = \begin-{bmatrix}x \ y\end-{bmatrix}$ 做变换, 所以也能表示为下列形式:
$T = A \begin-{bmatrix}x \ y\end-{bmatrix} + B$ or $T = M ^{T}$
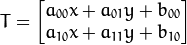
$T=\begin-{bmatrix}a_{00}x + a_{01}y + b_{00} \ a_{10}x + a_{11}y + b_{10}\end-{bmatrix}$ 　　

而在冈萨雷斯的《数字图像处理_第三版》里有：

最常用的空间坐标变换之一是仿射变换，其一般形式如下： \[ \begin{bmatrix} x & y & 1 \end{bmatrix} = \begin{bmatrix} v & w & 1 \end{bmatrix} \textbf{T} = \begin{bmatrix} v & w & 1 \end{bmatrix} \begin{bmatrix} t_{11} & t_{12} & 0 \\ t_{21} & t_{22} & 0 \\ t_{31} & t_{32} & 1 \end{bmatrix} \] 其中 $(v,w)$ 为原坐标，$(x,y)$ 为变换后的坐标，可根据变换矩阵 $\textbf{T}$ 中的元素选择的值，对一组坐标点做尺度、旋转、平移或偏移变换。一些常见的变换矩阵及作用如下表：
变换名称仿射变换矩阵$\textbf{T}$ 坐标公式
恒等变换 $\begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{bmatrix}$ $\begin{cases} x=v , \\ y=w \end{cases}$
尺度变换 $\begin{bmatrix} c_x & 0 & 0 \\ 0 & c_y & 0 \\ 0 & 0 & 1 \end{bmatrix}$ $\begin{cases} x=vc_x , \\ y=wc_y \end{cases}$
旋转变换（以逆时针为正） $\begin{bmatrix} cos(\theta) & sin(\theta) & 0 \\ -sin(\theta) & cos(\theta) & 0 \\ 0 & 0 & 1 \end{bmatrix}$ $\begin{cases} x=vcos(\theta)-wsin(\theta) , \\ y=vsin(\theta)+wcos(\theta) \end{cases}$
旋转变换（以顺时针为正） $\begin{bmatrix} cos(\theta) & -sin(\theta) & 0 \\ sin(\theta) & cos(\theta) & 0 \\ 0 & 0 & 1 \end{bmatrix}$ $\begin{cases} x=vcos(\theta)+wsin(\theta) , \\ y=-vsin(\theta)+wcos(\theta) \end{cases}$
平移变换 $\begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ t_x & t_y & 1 \end{bmatrix}$ $\begin{cases} x=v+t_x , \\ y=w+t_y \end{cases}$
偏移变换（水平） $\begin{bmatrix} 1 & 0 & 0 \\ s_h & 1 & 0 \\ 0 & 0 & 1 \end{bmatrix}$ $\begin{cases} x=v+ws_h , \\ y=w \end{cases}$
偏移变换（垂直） $\begin{bmatrix} 1 & s_v & 0 \\\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{bmatrix}$ $\begin{cases} x=v , \\ y=vs_v+w \end{cases}$
仿射变换的实现由两种方式：一种是 前向映射（Forward Mapping）：直接采用利用原图像坐标 $(v,w)$ 通过 $\begin{bmatrix} x & y & 1\end{bmatrix}=\begin{bmatrix} v & w & 1\end{bmatrix} \textbf{T}$ 得到变换后的坐标 $(x,y)$，使用前向映射会导致一些问题：可能会有多个像素坐标映射到输出图像的同一位置，也可能输出图像的某些位置完全没有相应的输入图像像素与它匹配，也就是没有被映射到，造成有规律的空洞（黑色的花纹状）；更好的一种方式是采用 反向映射（Inverse Mapping）：扫描输出图像的位置 $(x,y)$，通过 $\begin{bmatrix} v & w & 1\end{bmatrix}= \begin{bmatrix} x & y & 1\end{bmatrix}\textbf{T}^{-1}$（其中 $\textbf{T}^{-1}$ 为 $\textbf{T}$ 的逆矩阵）计算输入图像对应的位置 $(v,w)$，通过插值方法决定输出图像该位置的灰度值。

变换名称	仿射变换矩阵\(\textbf{T}\)	坐标公式
恒等变换	\(\begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{bmatrix}\)	\(\begin{cases} x=v , \\ y=w \end{cases}\)
尺度变换	\(\begin{bmatrix} c_x & 0 & 0 \\ 0 & c_y & 0 \\ 0 & 0 & 1 \end{bmatrix}\)	\(\begin{cases} x=vc_x , \\ y=wc_y \end{cases}\)
旋转变换（以逆时针为正）	\(\begin{bmatrix} cos(\theta) & sin(\theta) & 0 \\ -sin(\theta) & cos(\theta) & 0 \\ 0 & 0 & 1 \end{bmatrix}\)	\(\begin{cases} x=vcos(\theta)-wsin(\theta) , \\ y=vsin(\theta)+wcos(\theta) \end{cases}\)
旋转变换（以顺时针为正）	\(\begin{bmatrix} cos(\theta) & -sin(\theta) & 0 \\ sin(\theta) & cos(\theta) & 0 \\ 0 & 0 & 1 \end{bmatrix}\)	\(\begin{cases} x=vcos(\theta)+wsin(\theta) , \\ y=-vsin(\theta)+wcos(\theta) \end{cases}\)
平移变换	\(\begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ t_x & t_y & 1 \end{bmatrix}\)	\(\begin{cases} x=v+t_x , \\ y=w+t_y \end{cases}\)
偏移变换（水平）	\(\begin{bmatrix} 1 & 0 & 0 \\ s_h & 1 & 0 \\ 0 & 0 & 1 \end{bmatrix}\)	\(\begin{cases} x=v+ws_h , \\ y=w \end{cases}\)
偏移变换（垂直）	\(\begin{bmatrix} 1 & s_v & 0 \\\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{bmatrix}\)	\(\begin{cases} x=v , \\ y=vs_v+w \end{cases}\)

　　本文这里采取冈萨雷斯的《数字图像处理_第三版》的变换矩阵方式，毕竟所学的矩阵论也是将变换矩阵放在后面作为第二个因子。虽然仿射变换都有现成的 API 可以调用，而且速度一般要比自己写的要快，但是知其然终究也要知其所以然。

　　下面就以旋转变换为例了，因为尺度变换和平移变换只需要相应的缩放图像即可，而旋转变换不仅需要更改图像大小，还要确定旋转中心，而旋转中心一般以图像中心为标准。

旋转变换

　　旋转变换首先需要确定旋转中心，若以图像左上角为旋转中心，则只需要像做尺度变换和平移变换那样通过 $\begin{bmatrix} v & w & 1\end{bmatrix}= \begin{bmatrix} x & y & 1\end{bmatrix}\textbf{T}^{-1}$ 做普通的变换即可。而以图像中心为旋转中心，首先需要做坐标变换，将以左上角为原点，水平向右为 X 轴，垂直向下为 Y 轴的图像坐标系转换为以图像中心为原点，水平向右为 X 轴，垂直向下为 Y 轴的数学坐标系；再做正常的旋转变换；随后再将数学坐标系转换为图像坐标系，所以图像中心为旋转中心的旋转变换总共需要做三次变换。这里就以图像中心为旋转中心为例，由于有三次变换，所以应该有三个变换矩阵相乘，设图像坐标系==》数学坐标系的变换矩阵为 T1，旋转变换矩阵为 T2，数学坐标系==》图像坐标系的变换矩阵为 T3，设顺时针旋转角度为 $\theta$ ，原图像宽度为 $C$，高度为 $R$，旋转后图像宽度为 $W$，高度为 $H$，则： \[ T1=\begin{bmatrix} 1 & 0 & 0 \\ 0 & -1 & 0 \\ -0.5C & 0.5R & 1 \end{bmatrix}　　 T2=\begin{bmatrix} cos(\theta) & -sin(\theta) & 0 \\ sin(\theta) & cos(\theta) & 0 \\ 0 & 0 & 1 \end{bmatrix}　　 T3=\begin{bmatrix} 1 & 0 & 0 \\ 0 & -1 & 0 \\ 0.5W & 0.5H & 1 \end{bmatrix} \] 则旋转变换最终形式为：$\begin{bmatrix} x & y & 1 \end{bmatrix}=\begin{bmatrix} v & w & 1\end{bmatrix} \textbf{T}=\begin{bmatrix} v & w & 1 \end{bmatrix}T1*T2*T3$。

※BTW：旋转变换中，旋转后图像宽度 $W$，高度 $H$ 与原图像宽度 $C$，高度 $R$ 的关系为： \[ \begin{cases} H = |R*cos(\theta)| + |C*sin(\theta)| , \\ W = |C*cos(\theta)| + |R*sin(\theta)| \end{cases} \]

插值篇

　　因为经过采用反向映射¹方式的仿射变换之后，得到的原图像坐标 $(v,w)$ 往往不是整数值，所以无法知道其对应的像素值 $f(w,v)$，这时需要采取插值的方式近似估计该坐标位置的像素值。

　　常用的插值方法有最近邻插值（nearest neighbor interpolation）、双线性插值（bilinear interpolation）和双三次插值（bicubic interpolation），其中双三次插值在保持图像细节方面最好，但花费时间也最多，PS 中的消除锯齿和羽化效果好像就采用了双三次插值。

　　最近邻插值只考虑相邻最近的像素，双线性插值考虑相邻的 4 个像素点，双三次插值则考虑相邻的 16 个像素点。

双线性插值

　　双线性插值是线性插值方法的一种扩展，它是 X 和 Y 两个方向上线性插值的组合。

如上图，设变换后图像的坐标 $(x,y)$ 通过反向映射得到原图像坐标 $(v,w)$ ，即点 $P$ 正好处于四个像素点 $P1(v_0, w_0)$、$P2(v_0+1, w_0)$、$P3(v_0+1, w_0+1)$、$P4(v_0, w_0+1)$ 的中间，其中 $v_0=⌊v⌋$，$w_0=⌊w⌋$ ，点 $P$ 对应的像素值为 $f(P)$ 因为双线性插值即在 $X$ 和 $Y$ 两个方向进行线性插值，首先计算 $X$ 方向的插值： \[ \begin{cases} \frac{f(P2)-f(P1)}{P2.x-P1.x}=\frac{f(Z1)-f(P1)}{Z1.x-P1.x} , \\ \frac{f(P3)-f(P4)}{P3.x-P4.x}=\frac{f(Z2)-f(P4)}{Z2.x-P4.x} \end{cases} \] 即： \[ \begin{cases} f(Z1)=\frac{Z1.x-P1.x}{P2.x-P1.x}f(P2)+\frac{P2.x-Z1.x}{P2.x-P1.x}f(P1) =(v-v_0)f(P2)+(v_0+1-v)f(P1), \\ f(Z2)=\frac{Z2.x-P4.x}{P3.x-P4.x}f(P3)+\frac{P3.x-Z2.x}{P3.x-P4.x}f(P4) =(v-v_0)f(P3)+(v_0+1-v)f(P4) \end{cases}\tag{1} \] 然后计算 $Y$ 方向的插值： \[ \begin{equation} \frac{f(Z2)-f(Z1)}{Z2.y-Z1.y}=\frac{f(P)-f(Z1)}{P.y-Z1.y} \end{equation} \] 即： \[ \begin{equation} f(P)=\frac{P.y-Z1.y}{Z2.y-Z1.y}f(Z2)+\frac{Z2.y-P.y}{Z2.y-Z1.y}f(Z1) =(w-w_0)f(Z2)+(w_0+1-w)f(Z1) \end{equation}\tag{2} \] 结合式（1）和式（2）可得： \[ \begin{equation} f(P)=(v_0+1-v)(w_0+1-w)f(P1)+(v-v_0)(w_0+1-w)f(P2)+(v-v_0)(w-w_0)f(P3)+(v_0+1-v)(w-w_0)f(P4) \end{equation} \] 用矩阵形式可表示为： \[ f(P)=\begin{bmatrix} v_0+1-v & v-v_0 \end{bmatrix} \begin{bmatrix} f(P1) & f(P4) \\ f(P2) & f(P3) \end{bmatrix} \begin{bmatrix} (w_0+1-w) \\ (w-w_0) \end{bmatrix} \] 即： \[ f(y,x)=f(w,v)=\begin{bmatrix} ⌊v⌋+1-v & v-⌊v⌋ \end{bmatrix} \begin{bmatrix} f(⌊w⌋,⌊v⌋) & f(⌊w⌋+1,⌊v⌋) \\ f(⌊w⌋,⌊v⌋+1) & f(⌊w⌋+1,⌊v⌋+1) \end{bmatrix} \begin{bmatrix} (⌊w⌋+1-w) \\ (w-⌊w⌋) \end{bmatrix} \]

双三次插值

　　如上图，双三次插值需要考虑相邻16个像素（4×4），用双三次插值重采样的图像更平滑并且更能保留图像细节，在这三种插值算法中，双三次插值效果最好，但处理速度最慢。同样设变换后图像的坐标 $(x,y)$ 通过反向映射得到原图像坐标 $(v,w)$ ，与其左上角相邻最近的点P11 坐标则为 $(⌊v⌋,⌊w⌋)$ ，该插值方法需要选取一个合适的插值基函数，参照维基百科 Bicubic interpolation 的一般为： \[ W(x) = \begin{cases} (a+2)|x|^3-(a+3)|x|^2+1 & \text{for } |x| \leq 1, \\ a|x|^3-5a|x|^2+8a|x|-4a & \text{for } 1 < |x| < 2, \\ 0 & \text{otherwise}, \end{cases} \] 其中 $a$ 一般取 -0.5 、-0.75 或 -1；则：$f(y,x)=f(w,v)=A*B*C$ ，其中： \[ A=\begin{bmatrix} W( v-(⌊v⌋-1) ) & W(v-⌊v⌋) & W( (⌊v⌋+1)-v ) & W( (⌊v⌋+2)-v ) \end{bmatrix} \\ B=\begin{bmatrix} f(⌊w⌋-1,⌊v⌋-1) & f(⌊w⌋,⌊v⌋-1) & f(⌊w⌋+1,⌊v⌋-1) & f(⌊w⌋+2,⌊v⌋-1) \\ f(⌊w⌋-1,⌊v⌋) & f(⌊w⌋,⌊v⌋) & f(⌊w⌋+1,⌊v⌋) & f(⌊w⌋+2,⌊v⌋) \\ f(⌊w⌋-1,⌊v⌋+1) & f(⌊w⌋,⌊v⌋+1) & f(⌊w⌋+1,⌊v⌋+1) & f(⌊w⌋+2,⌊v⌋+1) \\ f(⌊w⌋-1,⌊v⌋+2) & f(⌊w⌋,⌊v⌋+2) & f(⌊w⌋+1,⌊v⌋+2) & f(⌊w⌋+2,⌊v⌋+2) \end{bmatrix} \\ C=\begin{bmatrix} W( w-(⌊w⌋-1) ) \\ W(w-⌊w⌋) \\ W( (⌊w⌋+1)-w ) \\ W( (⌊w⌋+2)-w ) \end{bmatrix} \]

即： \[ f(y,x)=f(w,v)= \sum\limits_{row=-1}^2\sum\limits_{col=-1}^2f(⌊w⌋+row,⌊v⌋+col)W(row-(w-⌊w⌋))W(col-(v-⌊v⌋)) \] 另附：网上也有人中间那个矩阵 $B$ 是本文中间矩阵 $B$ 的转置，经过下文实践，感觉效果差不多，但从理论上来说，应该本文这样写才是对的吧🤔。

Lanczos 插值

　　Lanczos 插值和双三次插值本质上差不多，不同的是插值权重基函数不一样，Lanczos 插值算法的基函数为： \[ L(x) = \begin{cases} 1 & \text{for } x = 0, \\ a*sin(\pi x)sin(\pi x/a)/(\pi x)^2 & \text{for } 0 < |x| \leq a, \\ 0 & \text{otherwise}, \end{cases} \] 其中 a 代表插值窗口半径，若 a = 2，则代表取周围 4×4 邻域像素点进行插值，和双三次插值除权重不一样外其它都一样，此时适用于对图像下采样（缩小），若 a = 3，则代表取周围 9×9 邻域像素点进行插值，此时适用于对图像上采样（放大），OpenCV 的 INTER_LANCZOS4 插值参数就代表取周围 8×8 邻域的像素点进行插值。

实践篇

　　本次实践采用 Matlab R2016b，具体 matlab 实现代码为：

clc;clear;close all;

img = imread('lena_gray.jpg'); % 读取图像
[R, C] = size(img); % 获取图像大小

theta = 45 * pi / 180.0; % 旋转角度
H = ceil(abs(R*cos(theta)) + abs(C*sin(theta)));    % 变换后图像的高度
W = ceil(abs(C*cos(theta)) + abs(R*sin(theta)));    % 变换后图像的宽度
res = zeros(H, W);   % 构造结果矩阵。每个像素点默认初始化为0（黑色）

T1 = [1 0 0; 0 -1 0; -0.5*C 0.5*R 1];   % 将原图像坐标映射到数学笛卡尔坐标
T2 = [cos(theta) -sin(theta) 0; sin(theta) cos(theta) 0; 0 0 1];    % 数学笛卡尔坐标下顺时针旋转的变换矩阵
T3 = [1 0 0; 0 -1 0; 0.5*W 0.5*H 1];    % 将数学笛卡尔坐标映射到旋转后的图像坐标
T = T1*T2*T3;
inv_T = inv(T);    % 求逆矩阵
% inv_T = [cos(theta) -sin(theta) 0; sin(theta) cos(theta) 0; -0.5*W*cos(theta)-0.5*H*sin(theta)+0.5*C 0.5*W*sin(theta)-0.5*H*cos(theta)+0.5*R 1];

for y = 1 : H   % 变换后图像的纵坐标，行，高
    for x = 1 : W   % 变换后图像的横坐标，列，宽
        original_coordinate = [x y 1] * inv_T; % 矩阵乘法
        v = original_coordinate(1);    % 原图像的横坐标，列，宽
        w = original_coordinate(2);    % 原图像的纵坐标，行，高
        % 变换后的位置判断是否越界
        if v>=1 && w>=1 && v<=C && w<=R
            res(y, x) = img(round(w), round(v));  % 用原图像对应坐标的像素值填充变换后的图像（最邻近插值）
            
            % ------------- 双线性插值（bilinear interpolation）-----------------
            left = floor(v); right = ceil(v); top = floor(w); bottom = ceil(w);
            dC = v-left;   % 列偏差
            dR = w-top;    % 行偏差
            res(y, x) = (1-dC)*(1-dR)*img(top, left) + dC*(1-dR)*img(top,right) + (1-dC)*dR*img(bottom, left) + dC*dR*img(bottom, right); 
            
            % ------------- 双三次插值（bicubic interpolation） -------------------------
        if left>=2 && top>=2 && left<=(C-2) && top<=(R-2)
            img = double(img);
            MA = [bicubic(1+dC) bicubic(dC) bicubic(1-dC) bicubic(2-dC)];
            MB = [img(top-1,left-1) img(top,left-1) img(top+1,left-1) img(top+2,left-1);
                 img(top-1,left) img(top,left) img(top+1,left) img(top+2,left);
                 img(top-1,left+1) img(top,left+1) img(top+1,left+1) img(top+2,left+1);
                 img(top-1,left+2) img(top,left+2) img(top+1,left+2) img(top+2,left+2)];
            % MB = MB';    % 求转置矩阵
            MC = [bicubic(1+dR); bicubic(dR); bicubic(1-dR); bicubic(2-dR)];
            res(y, x) = MA*MB*MC;
        end
        end
    end
end;

figure, imshow(uint8(res)); % 显示图像

BiCubic 基函数 Matlab 代码为：

function W = bicubic(x)
%bicubic 双三次插值基函数
a = -1; % 默认取a为-1
x1 = abs(x);
x2 = x1*x1;
x3 = x1*x2; 

if x1 <= 1
   W = 1 - (a+3)*x2 + (a+2)*x3;
elseif x1>1 && x1<=2
   W = -4*a + 8*a*x1 - 5*a*x2 + a*x3;
else 
   W = 0;
end

　　旋转变换中感觉插值的作用没体现出来，以肉眼来看感觉三种插值方法的效果差不多，可能是 Shaun 选取的示例不好，为了体现插值效果，应该采用尺度变换（缩放变换）的。以上代码改为尺度变换也简单，自定义图像缩放后的宽高，以两倍为例，H = R * 2; W = C * 2;，再将旋转变换矩阵改为尺度变换矩阵，尺度变换矩阵中 $c_x=W/C；c_y=H/R$。

为了便于理解，Shaun 对代码就不进行优化了（其实是你懒吧 _(:з」∠)_）。

后记

　　本文算是数字图像处理中最基础的知识了，但 Shaun 在写时还是查阅了大量相关的资料，有些地方理解的还不是很透彻，行文思路有点混乱 ╮(╯▽╰)╭。本来是不想使用图片的，但本文不用图片很难理解清楚，又为了不使用外部图，最后只得参考 SVG 教程和如何创建SVG箭头和polymarker——marker元素采用 SVG 绘制相应图片了。等有时间再把用 OpenCV 实现的 C++ 代码也贴上吧。最后再感叹一下 Matlab 确实是做科研的好工具（°Д°）Ъ，~~吐槽一下 MathJax 排版好痛苦啊，太多需要转义符\的地方了吧。~~，搞错了 Σ(ﾟдﾟ;)，这主要和 markdown 渲染有关，hexo 默认的 markdown 渲染插件 hexo-renderer-marked 太普通了，有些东西根本没办法渲染或者渲染有问题（╯‵□′）╯︵┴─┴，Shaun 最后决定使用 hexo-renderer-pandoc 插件渲染 markdown，这样就完美了 (๑•̀ㅂ•́)و✧ 。

　　至于具体怎么使用 hexo-renderer-pandoc 替换默认的渲染器可参考：如何禁止 hexo 在 html 代码里插入<br>标签?。具体如下：

# 1、安装 Pandoc，可以不顺带安装 MiKTex
# 2、卸载默认渲染器
npm uninstall hexo-renderer-marked --save
# 3、安装 hexo-renderer-pandoc
npm install hexo-renderer-pandoc --save

附录

　　挖的坑总是要填的，呐，这就是用 OpenCV 实现的旋转变换，实现语言为 C++ ：

#include <opencv2/opencv.hpp>

#define M_PI       3.14159265358979323846

double bicubic(double x)
{
	// bicubic 双三次插值基函数
	int a = -1;	// 默认取a为 - 1
	double x1 = fabs(x);
	double x2 = x1*x1;
	double x3 = x1*x2;

	if (x1 <= 1)
	{
		return 1 - (a + 3)*x2 + (a + 2)*x3;
	}
	else if (x1 > 1 && x1 <= 2)
	{
		return -4 * a + 8 * a*x1 - 5 * a*x2 + a*x3;
	}
	else
	{
		return 0;
	}
}

int main(int argc, char *argv[])
{
	cv::Mat img = cv::imread("../Data/lena_gray.jpg", 0);	// 以灰度模式读取图片

	int R = img.rows;	// 获取原图像高度
	int C = img.cols;	// 获取原图像宽度

	double theta = 45 * M_PI / 180.0;	// 旋转角度

	int H = ceil(fabs(R*cos(theta)) + fabs(C*sin(theta)));	// 变换后图像的高度
	int W = ceil(fabs(C*cos(theta)) + fabs(R*sin(theta)));	// 变换后图像的宽度

	cv::Mat res = cv::Mat::zeros(H, W, CV_8UC1);	// 构造结果矩阵。每个像素点默认初始化为0（黑色）	

	cv::Mat T1 = (cv::Mat_<double>(3, 3) << 1, 0, 0, 0, -1, 0, -0.5*C, 0.5*R, 1);	// 将原图像坐标映射到数学笛卡尔坐标
	cv::Mat T2 = (cv::Mat_<double>(3, 3) << cos(theta), -sin(theta), 0, sin(theta), cos(theta), 0, 0, 0, 1);	// 数学笛卡尔坐标下顺时针旋转的变换矩阵
	double t3[3][3] = { { 1, 0, 0 }, { 0, -1, 0 }, { 0.5*W, 0.5*H, 1 } };	// 将数学笛卡尔坐标映射到旋转后的图像坐标
	cv::Mat T3 = cv::Mat(3, 3, CV_64FC1, t3);
	cv::Mat T = T1*T2*T3;
	cv::Mat inv_T = T.inv();	// 求逆矩阵
	//cv::Mat inv_T = (cv::Mat_<double>(3, 3) << cos(theta), -sin(theta), 0, sin(theta), cos(theta), 0, -0.5*W*cos(theta) - 0.5*H*sin(theta) + 0.5*C, 0.5*W*sin(theta) - 0.5*H*cos(theta) + 0.5*R, 1);

	for (int y = 0; y < H; y++)
	{
		for (int x = 0; x < W; x++)
		{
			cv::Mat point = (cv::Mat_<double>(1, 3) << x, y, 1);
			cv::Mat original_coordinate = point * inv_T;	// 矩阵乘法
			double v = original_coordinate.at<double>(0, 0);	// 原图像的横坐标，列，宽
			double w = original_coordinate.at<double>(0, 1);	// 原图像的纵坐标，行，高

			// 变换后的位置判断是否越界
			if (v >= 0 && w >= 0 && v <= C - 1 && w <= R - 1)
			{
				res.at<uchar>(y, x) = img.at<uchar>(round(w), round(v));	// 用原图像对应坐标的像素值填充变换后的图像（最邻近插值）
				
				// ------------ - 双线性插值（bilinear interpolation）---------------- -
				int left = floor(v), right = ceil(v), top = floor(w), bottom = ceil(w);
				double dC = v - left;	// 列偏差
				double dR = w - top;	// 行偏差
				res.at<uchar>(y, x) = (1 - dC)*(1 - dR)*img.at<uchar>(top, left) + dC*(1 - dR)*img.at<uchar>(top, right) + (1 - dC)*dR*img.at<uchar>(bottom, left) + dC*dR*img.at<uchar>(bottom, right);
			
				// ------------ - 双三次插值（bicubic interpolation）------------------------ -
				if (left >= 1 && top >= 1 && left <= (C - 3) && top <= (R - 3))
				{
					cv::Mat MA = (cv::Mat_<double>(1, 4) << bicubic(1 + dC), bicubic(dC), bicubic(1 - dC), bicubic(2 - dC));
					cv::Mat MB = img(cv::Rect(left - 1, top - 1, 4, 4));	// 提取当前相邻区域16个像素点做插值
					MB.convertTo(MB, CV_64FC1);	// 变换为浮点型数据
					MB = MB.t();	// 求转置矩阵
					cv::Mat MC = (cv::Mat_<double>(4, 1) << bicubic(1 + dR), bicubic(dR), bicubic(1 - dR), bicubic(2 - dR));
					cv::Mat result = MA*MB*MC;
					res.at<uchar>(y, x) = static_cast<uchar>(result.at<double>(0, 0));
				}
			}
		}
	}

	cv::imshow("result", res);	// 显示变换后图像
	cv::waitKey(0);

	return 0;
}

　　以上 C++ 代码在 VS2013 下能完美运行，不管是用 OpenCV-2.4.11 还是 OpenCV-3.2.0。其实完全理解的话，不管用什么工具都能实现，只是看哪个工具方便一点而已，就这个而言，感觉 Matlab 要方便很多，Shaun 就不继续挖 Python 的坑了，毕竟如果要用 Python 实现其实还是用 OpenCV，只是用 OpenCV Python 版的接口而已。

参考资料

[１] 第4章图像几何变换

[２] 图像旋转原理及实现

[３] 仿射变换（http://www.opencv.org.cn/opencvdoc/2.3.2/html/doc/tutorials/tutorials.html）

[４] 图像处理常用插值方法总结

[５] Wikipedia Bilinear interpolation

[６] 双线性插值算法的详细总结

[７] Wikipedia Bicubic interpolation

[８] 双三次插值(bicubic interpolation)原理及MATLAB源码实现

[９] 图像缩放】双立方（三次）卷积插值（https://dailc.github.io/blog/tags.html#%E6%8F%92%E5%80%BC%E7%AE%97%E6%B3%95）

为啥不说前向映射呢？这是因为若原图像坐标 $(v,w)$ 通过前向映射方式得到变换后图像的坐标 $(x,y)$ ，而且这个坐标为小数的话，一般采用四舍五入的方式得到变换后图像对应的整数坐标 $(⌊x+0.5⌋,⌊y+0.5⌋)$，令 $f(⌊y+0.5⌋,⌊x+0.5⌋)=f(w,v)$ 。↩︎
$⌊x⌋$ 表示向下取整，称为 Floor，指的是小于或等于 $x$ 的最大整数；$⌈x⌉$ 表示向上取整，称为 Ceil，指的是大于或等于 $x$ 的最小整数，$eg：⌊5.6⌋ = 5，⌊-5.6⌋ = -6；⌈5.6⌉ = 6，⌈-5.6⌉ = -5。$↩︎